Resitores em Série e Paralelo |
Voltar à página principal |
Resitores em Série e Paralelo |
Voltar à página principal |
![]() Resistência e Resistividade Elétrica
Resistência e Resistividade Elétrica
Experimentalmente encontra-se que em um metal, à temperatura constante, a densidade de corrente é diretamente proporcional ao campo elétrico aplicado, então,
![]() (6)
(6)
onde s é uma constante denominada
de condutividade. Assim, quanto maior for a condutividade de um material
menor deve ser o campo E para criar uma mesma densidade de corrente J.
A constante s(E), algumas vezes é
função do campo elétrico aplicado.
O recíproco da condutividade
é chamado de resistividade r ,
então;
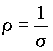 (7)
(7)
usando este resultado obtemos que,
![]() (8)
(8)
Na tabela 1, apresentamos alguns valores característicos de resistividades
de certos materiais.
|
|
|
|
|
|
||
| Prata |
|
|
| Cobre |
|
|
| Alumínio |
|
|
| Tungstênio |
|
|
| Ferro |
|
|
|
|
||
| Carbono (grafite) |
|
|
| Germânio |
|
|
| Silício |
|
|
|
|
||
| Vidro |
|
|
| Borracha |
|
Tabela 1 - Resistividade de alguns materiais
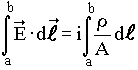 (15)
(15)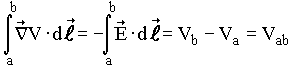 (16)
(16)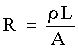 (17)
(17)A resistividade de um material depende, entre outras coisas, da temperatura. Em geral, a resistência dos metais aumentam com a temperatura. Isto não é uma surpresa, pois com o aumento da temperatura os átomos se movem mais rapidamente dentro do material, promovendo com isto o crescimento dos choques entre os elétrons livres e os átomos. Se a temperatura não varia muito, podemos dizer que a resistividade dos metais aumentam linearmente com a temperatura. Isto é,
![]() (9)
(9)
Observa-se experimentalmente que condutores feitos do mesmo material, mas que diferem pelos comprimentos e pelas áreas das seções transversais têm maior resistência ao movimento dos elétrons no condutor. Verifica-se também que, condutores com a mesma seção transversal, têm maior resistência aqueles de maior comprimento L. Isto é,
(10)
Por outro lado, para condutores de mesmo comprimento, tem maior resistência o fio de menor área de seção transversal.
(11)
Estes resultados leva-nos a concluir a resistência elétrica ( R ) é uma grandeza que depende das caracteristicas do material (resistividade), assim como de suas dimensões (L e A). Dados experimentais mostram que a resistência (R) de fios condutores de um dado material é diretamente proporcional ao comprimento (L) do fio e inversamente proporcional à área (A) da seção transversal do fio, como mostra a equação abaixo,
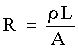 (12)
(12)
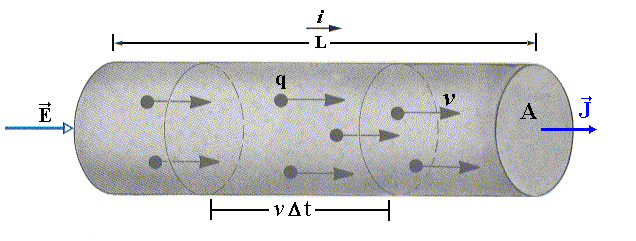
Fig.1 - Fio condutor
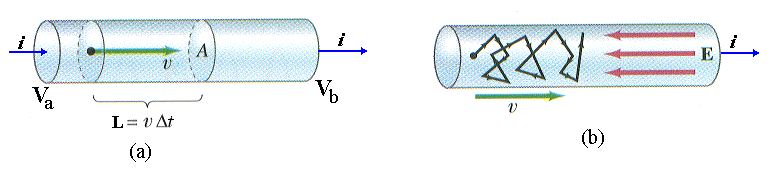
Fig. 2 - Resistência à passagem de elétrons no
interior do condutor
Vimos que a resistividade de um material depende da temperatura, aumentando quando se aquece o condutor, na maior parte dos casos. Assim, quando a temperatura de um fio condutor aumente, geralmente sua resistência aumenta em vista do aumento da resistividade da substância que o constitui. A variação da resistência por dilatação do fio pode ser desconsiderada. Estes resultados leva-nos a concluir que a resistência elétrica também deve depender da temperatura. Pode-se mostrar isto, substituindo a Eq.(9) em (12), isto é
![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Aug/24/99
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Register No 169.766 -
Biblioteca Nacional - Ministério da Cultura