Campo Elétrico em Isolantes |
Voltar à página principal |
Campo Elétrico em Isolantes |
Voltar à página principal |
O conceito de energia, em mecânica, mostrou-se ser de suma importância no estudo de problemas nesta área da física, principalmente naqueles casos onde os cálculos envolvendo as leis de Newton têm solução complexa.
No caso da eletrostática o conceito de energia é também especialmente valioso. Ele não somente estende a lei de conservação, mas também permite-nos ver o fenômeno eletrostático de um outro ponto de vista, fornecendo assim, uma ferramenta poderosa na solução de problemas. Em muitos problemas eletrostático, a solução fica mais simples quando usamos relações envolvendo a energia, do que aplicando as leis envolvendo a força e o campo elétrico.
Para aplicar a conservação
da energia, necessitamos definir o conceito de energia potencial elétrica,
como tem sido feito para o caso de outras energias potenciais, por exemplo
a gravitacional. Isto pode ser feito analisando o trabalho realizado para
mover uma carga de prova qo na presença de um campo elétrico
externo.
Ao abandonar-se, em repouso,
uma carga elétrica q, puntiforme, nume região onde existe
um campo elétrico isolado, ela fica sujeita a uma força elétrica
resultante F e desloca-se espontaneamente na direção e sentido
desta força. Nestas condições, o trabalho realizado
por F é sempre positivo.
Com relação
à forma da trajetória descrita pela carga qo nada
se pode prever, pois a direção da força F é
variável (tangente a uma linha de força ou linha de campo
em cada ponto). Não se deve afirmar que a trajetória da partícula
coincide com uma linha de força, a menos que esta seja retilínea.
O movimento da partícula se dará sempre no sentido da força
F.
Durante o movimento espontâneo
da partícula q verificam-se algumas propriedades que se seguem:
| Em todo movimento espontâneo de carga elétrica, na presença de campo elétrico, a energia potencial elétrica da mesma diminui. |
| Cargas elétricas positivas, abandonadas em repouso na presença de campo elétrico e sujeitas apenas à ação da força elétrica, deslocam espontaneamente para pontos de menor potencial elétrico. Se a carga for negativa o deslocamento se dará no sentido de maior potencial elétrico. |
O trabalho ()
realizado, sobre uma partícula de prova qo, para provocar
um pequeno deslocamento
é definido pelo produto escalar entre o vetor força F e o
vetor deslocamento, como a seguir:
(1)
Neste caso o trabalho é igual a diferença de energia gasta
para mover a carga de prova qo de um certo ponto a outro.
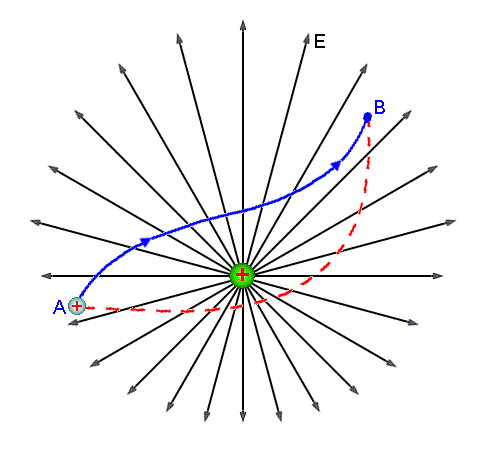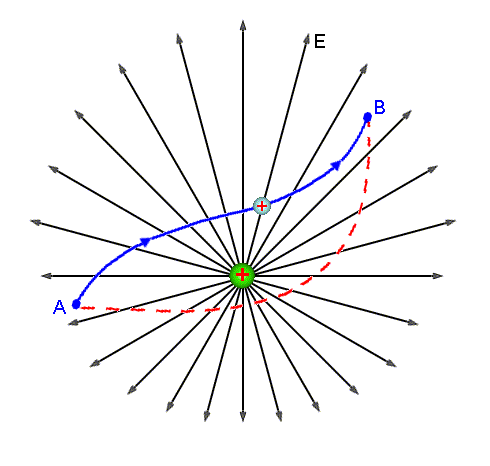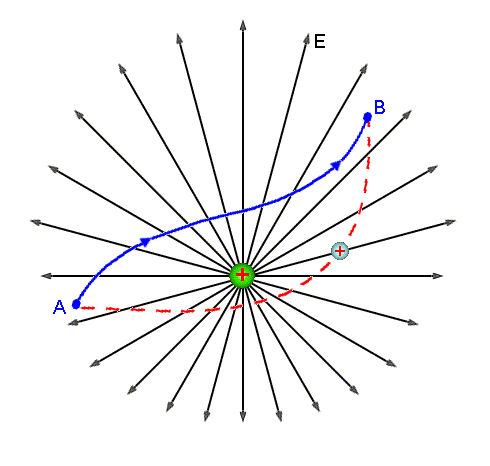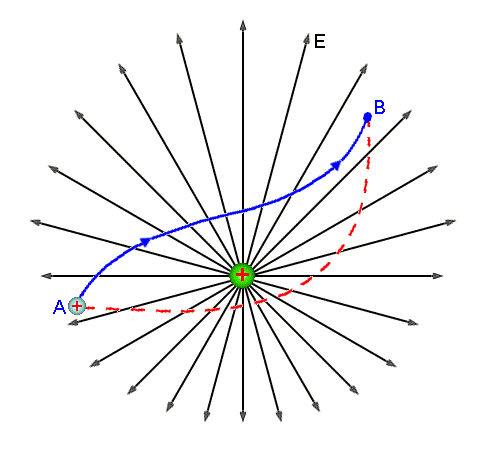
Supomos agora, que a partícula qo é forçada
a deslocar de um ponto A a um outro ponto B, na presença de um campo
elétrico, não necessariamente uniforme. Veja Fig.1
Pela a lei de Coulomb podemos escrever a força sobre a partícula em termos do campo elétrico, isto é,
![]() (2)
(2)
podemos ainda escrever esta relação explicitando as componentes vetoriais da força em termos do campo elétrico, então,
(2a)
Substituindo a equação (2) em (1), obtemos o trabalho
realizado em função do campo elétrico ![]() ,
isto é;
,
isto é;
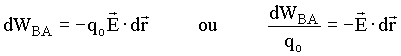 (3)
(3)
No capítulo anterior, definimos o conceito de campo elétrico como sendo igual a força por unidade de carga, no sentido de torná-lo uma grandeza independente da carga de prova qo, ou melhor falando, ser dependente apenas da distribuição de cargas elétricas que está criando o campo E. De forma semelhante, vamos introduzir o conceito de potencial elétrico como sendo uma grandeza independente de qo, como mostra a segunda equação em (5). Isto é;
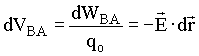 (5)
(5)onde
é diferença de potencial elétrico entre dois pontos,
no eixo x, em uma região do espaço contendo um campo elétrico.
Ë importante notar que as grandezas
não são componentes de um vetor, pois o potencial elétrico,
de acordo com a definição dada na eq.(5) é uma grandeza
escalar e não vetorial.
Integrando ambos lados da eq.(5), temos que;
| O potencial elétrico é definido crescente no sentido da linha de força ou linha de campo |
Vimos que o campo elétrico
foi introduzido aqui com o propósito de discutir a energia de uma
carga elementar (carga muito pequena) ao deslocar-se de um ponto a outro
no espaço contendo um campo elétrico. O caso mais simples
deste tipo interação é o de uma carga elementar q1
se movendo na presença de uma outra carga q2. Esta
questão foi indiretamenta tratada quando falamos sobre a lei de
Coulomb. Um outro ponto importante a destacar é que as interações
eletrostáticas guardam um certa semelhança com as gravitacionais.
A tabela abaixo mostra algumas das relações equivalentes.
|
|
|
|
|
|
| Gravitacional |
|
|
|
|
| Elétrica |
|
|
|
|
Observe que as expressões para as interações elétricas não contém o sinal negativa como na gravitacional. Isto significa que se as cargas q1 e q2 são ambas positivas ou negativas a interação entre elas será repulsiva, enquanto que se as cargas têm sinais opostos então a interação será atrativa. Isto não ocorre como caso gravitacional, onde as interações entre dois corpos massivos são sempre atrativas, por isto aparece o sinal negativo nas expressões.
De acordo com a definição
de diferença de potencial elétrico dada na Eq. (5), VBA
depende apenas do campo elétrico na região e consequentemente
da distribuição de cargas. Devemos lembrar que, mesmo tendo
introduzido o conceito de potencial, elétrico ou gravitacional,
apenas as diferenças de energias potenciais podem ser medidas experimentalmente.