Potencial e Energia Elétrica |
Voltar à página principal |
Potencial e Energia Elétrica |
Voltar à página principal |
![]() Potencial Elétrico Devido a uma Carga Puntiforme
Potencial Elétrico Devido a uma Carga Puntiforme
A diferença potencial entre dois pontos A e B devido a presença de uma carga puntiforme (Fig.1) é igual a
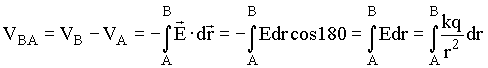

Neste caso, assumimos que a origem do sistema de coordenadas está localizado em cima da carga q. Isto significa que o potencial é infinito na origem e igual a zero no infinito. Lembramos que o potencial, como mostra a equação acima, é uma grandeza escalar.
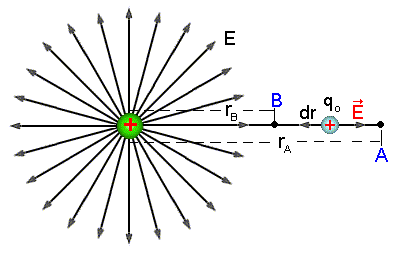
Fig.1 - Potencial devido a uma carga puntiforme
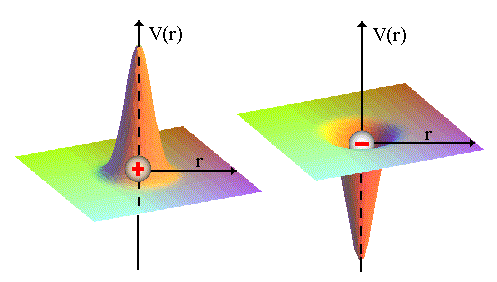
Fig.2 (a-b) Variação do potencial elétrico
criados por cargas positiva
e negativa em função distância.
As superfícies 3D (tri-dimensionais) das figuras 2a e 2b, são usadas para representar o comportamento do potencial elétrico, em termos da distância r, para duas cargas, uma positiva e outra negativa. As superfícies representam o potencial no plano (x,y,0). A medida que aproximamos do pontos onde as cargas estão localizadas, o potencial cresce rapidamente tendendo a +infinito, no caso de +q e a -infinito no caso de -q.
A unidade de potencial elétrico,
assim como da diferença de potencial, é Joules/Coulomb
[J/C] a qual é dada o nome de volt [1 V = 1 J/C], em
homenagem a Alessandro Volta (1745-1827). Volta ficou conhecido pela invenção
da bateria elétrica. A diferença de potencial elétrico
é freqüentemente referenciada por voltagem ou diferença
de de potencial (ddp).
De acordo com nossa definição
de diferença de potencial, veja Fig. 3(b), a placa positiva fica
a um potencial mais alto, quando comparado com o potencial da placa negativa.
Dessa forma um objeto carregado positivamente no interior das duas placas
da Fig.3(b), moverá naturalmente do potencial mais alto para o mais
baixo, isto é, da placa positiva para a negativa. Se desejamos falar
sobre o potencial em ponto A (VA), devemos levar em conta que
o valor VA vai depender escolha da origem de V. Freqüentemente
escolhemos o solo como sendo o ponto onde V é igual a zero. Algumas
vezes também, por conveniência de cálculo, escolhemos
o ponto V=0 no infinito. Veremos, a seguir, alguns exemplos onde este problema
aparecerá.
Como vimos anteriormente esta definição de potencial elétrico,
é análoga à definição para o potencial
gravitacional. A Fig.3, mostra esta analogia.
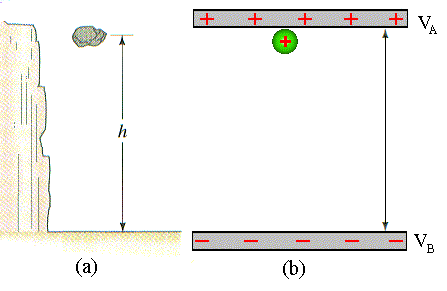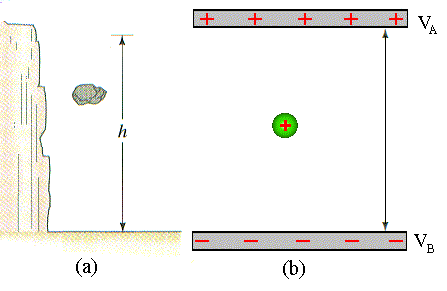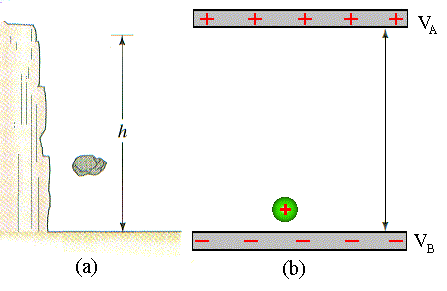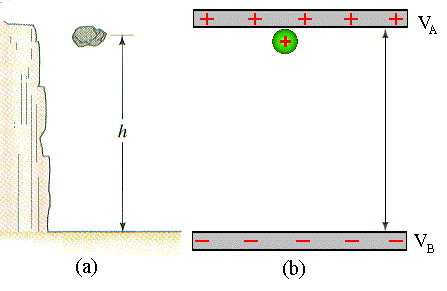
É interessante ressaltar que a diferença de potencial depende apenas pontos inicial e final. Isto implica que o trabalho realizado, para levar uma partícula do ponto A ao ponto B, independe do caminho. Veja figura 4.
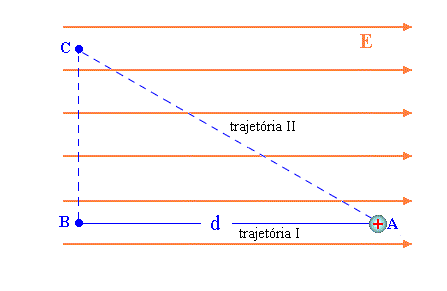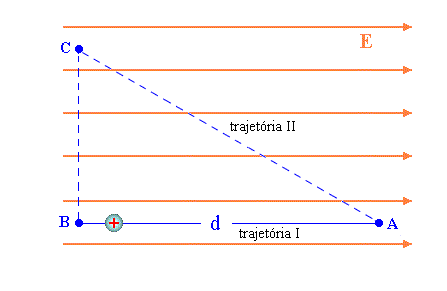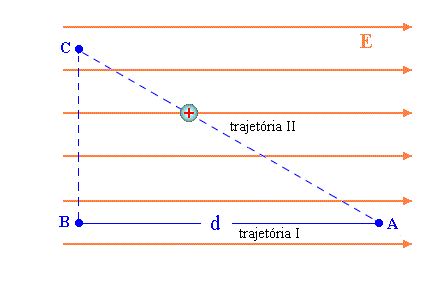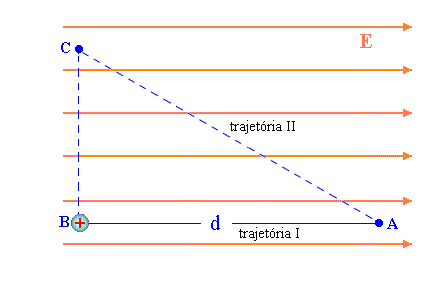
Isto pode ser facilmente verificado, analisando o trabalho realizado percorrendo as duas trajetórias da figura 4.
- Trajetória I :
Neste caso temos que a diferença
de potencial entre os pontos A e B é dada por;
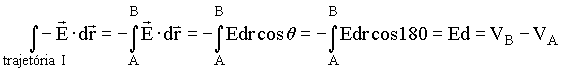 (9)
(9)
Assim a diferença de potencial entre os pontos A e B é igual a,
(10)
O ângulo entre os vetores
e
é
igual a 180o pois os dois vetores têm sentidos opostos.
Para esta trajetória a distância entre os pontos A e B é
igual a
.
- Trajetória II :
A diferença de potencial, para a trajetória II, pode ser calculada em duas etapas, a primeira entre os pontos A e C e a segunda entre os pontos C e B. Assim,
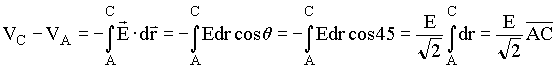 (11)
(11)ou
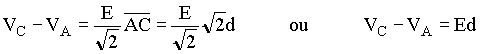 (12)
(12)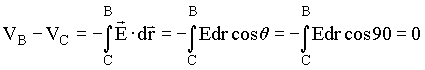 (13)
(13)