Potencial Elétrico de uma Carga |
Voltar à página principal |
Potencial Elétrico de uma Carga |
Voltar à página principal |
![]() Potencial Elétrico
para várias Distribuições de Cargas
Potencial Elétrico
para várias Distribuições de Cargas
![]() 1 - Distribuição Discreta de Cargas
1 - Distribuição Discreta de Cargas
No caso de uma distribuição de cargas discreta (Fig.1), o
campo elétrico pode ser calculado usando o princípio da
superposição. Isto significa que
o campo resultante, em um dado ponto do espaço, é igual a
soma dos campos elétricos
produzidos por cada carga individualmente no
ponto P. Isto é;
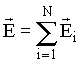 (14)
(14)
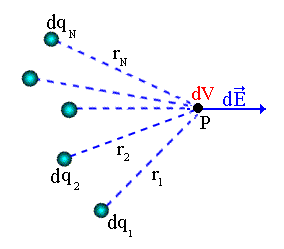
Logo, pela definição de potencial elétrico o potencial resultante em um ponto P, devido a uma distribuição de cargas discreta, será igual a soma algébrica dos potenciais em P devido a cada uma das cargas, isto é,
(15)
Como Vi é o potencial devido a uma carga puntiforme, veja seção anterior, temos que
(16)
![]() 2
- Potencial Elétrico Devido a um Conjunto de Cargas Puntiformes
2
- Potencial Elétrico Devido a um Conjunto de Cargas Puntiformes
Analisaremos a seguir o potencial elétrico devido a uma distribuição discreta de cargas, contendo quatro cargas posicionada nos vértices de um quadrado de lado d, como mostra a Fig.2.
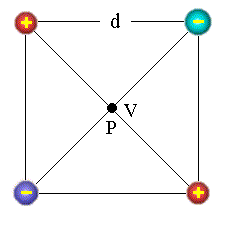
Neste caso o potencial no centro do quadrado (ponto P) é igual a soma algébrica dos potenciais devido a cada uma das quatro cargas, isto é,
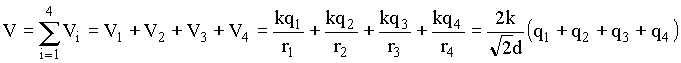
![]() 3
- O Potencial devido a um Dipolo Elétrico
3
- O Potencial devido a um Dipolo Elétrico
Discutimos, em seções anteriores, a importância da distribuição de cargas do tipo dipolar. O dipolo elétrico é definido como uma distribuição de duas cargas com sinais opostos separadas por uma distância a, veja Fig.3. Muitos sistemas físicos, na natureza, tem distribuições de cargas dipolares, a molécula de água é um exemplo clássico destes sistemas. Um vasilha contendo água pura, é um líquido dipolar, isto significa que podemos orientar as moléculas deste líquido aplicando um campo elétrico externo.
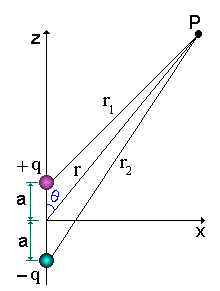
A seguir calcularemos o dipolo elétrico devido a uma distribuição deste tipo. Assim, o potencial V em um ponto P qualquer, será a soma dos potenciais criado em P por cada uma das cargas do dipolo, isto é;
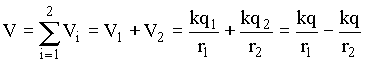 (18)
(18)
onde q1 = -q2 = q, e então,
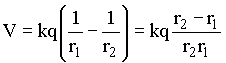 (19)
(19)
Com isto podemos calcular, também, o potencial em um ponto distante do dipolo. Neste caso temos que r >>a e portanto r2 - r1» 2acosq e ainda r2 » r1 pois a » 0. Assim,
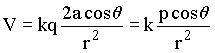 (20)
(20)
onde p é o momento dipolar.
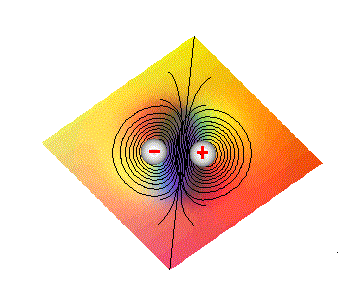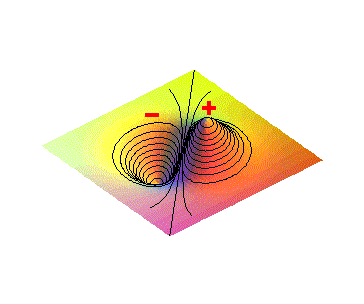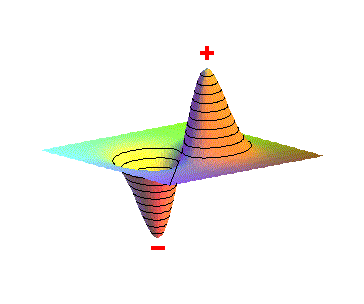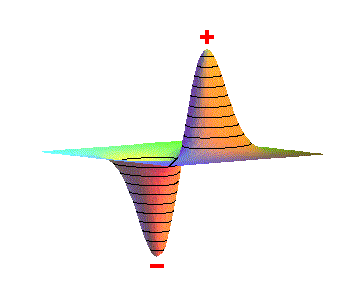
A superfície 3D (tri-dimensionais)
da Fig.4, é usada para representar o comportamento do potencial
elétrico, em termos da distância r, para um dipolo elétrico.
A superfície representa o potencial no plano (x,y,0). Observe que
a medida que aproximamos do pontos onde as cargas estão localizadas,
o potencial cresce rapidamente tendendo a +infinito,
no caso de +q e a -infinito
no caso de -q.