Potencial Elétrico:Exemplos |
Voltar à página principal |
Potencial Elétrico:Exemplos |
Voltar à página principal |
![]() Superfícies e Linhas
Equipotenciais
Superfícies e Linhas
Equipotenciais
O potencial elétrico pode ser representado por linhas equipotenciais e no caso de três dimensões por superfícies equipotenciais.
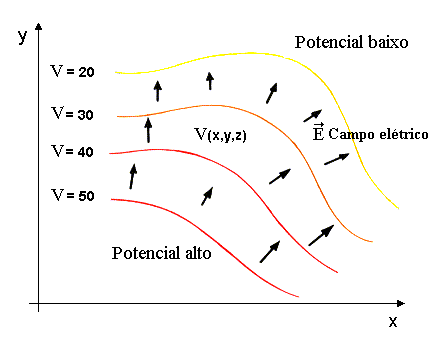
As
superfícies equipotenciais (S) são aquelas onde o potencial
elétrico é o mesmo em qualquer ponto de S. Isto significa
que a diferença de potencial entre dois pontos, pertencentes a esta
superfície, é igual a zero e portanto, o trabalho para deslocar
uma partícula carregada, sobre S, é nulo.
Uma conseqüência
da definição de superfície equipotencial é
que o campo E deve ser perpendicular S em qualquer ponto. Isto significa
que a componente do campo E, tangencial à superfície S, é
nula.Veja a seguir algumas equipotenciais para diferentes distribuições
de cargas.
O potencial, devido a uma carga puntiforme, depende da distância radial à carga. Assim, todos os pontos, em uma superfície esférica de raio R, têm o mesmo valor para o potencial. Isto significa que, espacialmente, as superfícies equipotenciais são esferas concêntricas. Em um plano, estas equipotenciais são círculos concêntricos como desenhado na Fig.2(a). As linhas contínuas, nas figuras Fig.2(c-b), representam as equipotenciais para um dipolo elétrico e duas cargas positivas, respectivamente. Nos três casos, Fig.2(a-c), o campo E é representado pelas linhas pontilhadas.
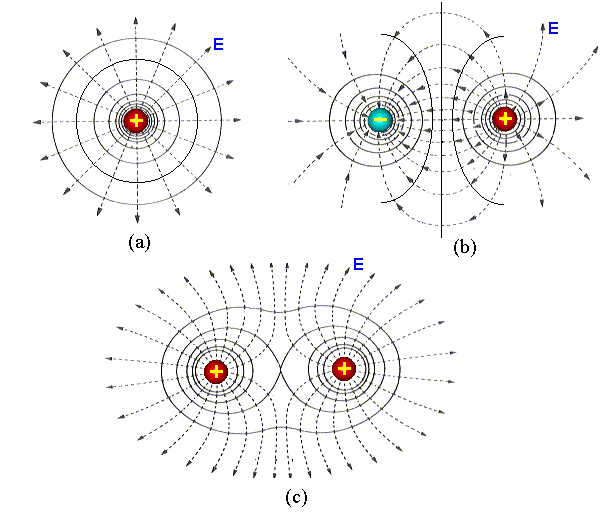
Fig. 2(a-c) -Equipotenciais para distribuição de cargas
discreta
A figura 3 mostra duas superfícies equipotenciais (S) geradas por um fio infinito carregado positivamente. A medida que afastamo-nos do fio, o potencial decresce. Anteriormente, mostramos que o campo elétrico gerado por um fio, é perpendicular a superfície lateral do fio, em qualquer ponto. Assim as equipotenciais são superfícies cilíndricas.
Usando ainda a Fig.3 podemos calcular a diferença de potencial em diferentes situações. Por exemplo, a diferença de potencial entre os pontos 1 e 2 é igual a zero pois os pontos 1 e 2 estão sobre uma superfície cujo potencial não varia. A diferença de potencial entre os pontos 3 e 4, também será nula pelo mesmo motivo anterior. Já no caso 5 e 6 , V é igual 40 volts, isto é V65 = V6 - V5 = 100V - 60V = 40V.
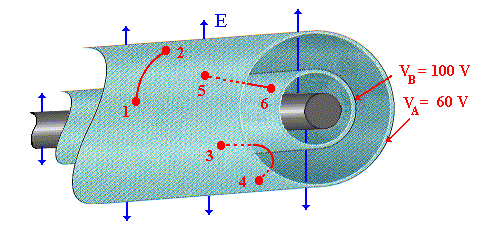
Fig.3 -Equipotenciais para distribuição de cargas linear
As figuras 4(a-b) mostram superfícies equipotenciais em torno de algumas ligações química em moléculas; a) ligação oxigênio-carbono no metanol e b) canal molecular de uma zeólita ou peneira molecular.
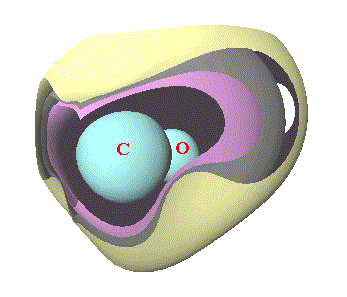
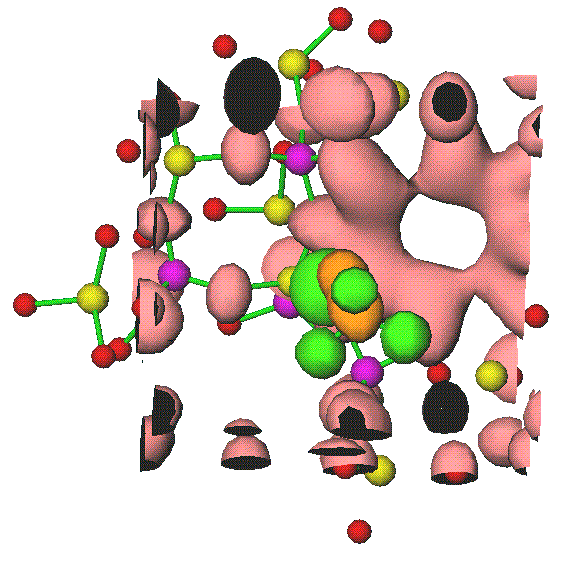
Fig. 4(a-b) -Equipotenciais para distribuição de cargas
volumétricas em sistema molecular
|
|
- Modo de usar :
- Selecione
o tipo de carga (positiva ou negativa) e sua intensidade de -5 à
+5 e.
- Click
com o mouse na janela para criar uma ou mais cargas
- Click
no botão "Potencial" para desenhar as linhas equipotenciais
- Click
na barra "3D-equipotenciais" para desenhar as superfícies equipotenciais
- Para limpar
a tela pressione o botão "Limpa Tela"
- Para simular
uma partícula se movendo na presença de uma distribuição
de carga
crie a distribuição de cargas e em seguida pressione o botão
"Animação"