Leis de Kirchhof |
Voltar à página principal |
Leis de Kirchhof |
Voltar à página principal |
![]() Aplicação das Leis de Kirchhoff
Aplicação das Leis de Kirchhoff
Observando o circuito da Fig.1, notamos que existem três correntes (i1, i2, i3) desconhecidas. A caracterização do circuito ficará completa com a determinação das correntes, isto é calcular as suas intensidades e sentidos de percurso em cada malha. Neste caso, é necessário construir três equações independentes, pois tem-se três incógnitas (i1, i2, i3).
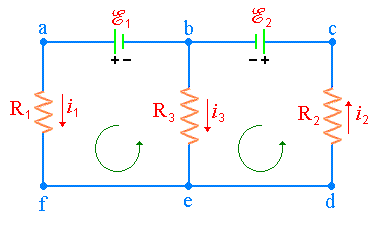
Fig.1 - Circuito elétrico com duas malhas
A solução deste problema pode ser encontrada usando as leis de conservação de Kirchhoff, como discutido acima. Os passos a seguir descrevem este procedimento;
O referido circuito tem dois nós, os pontos b e e , consequentemente existem duas equações;
![]() a)
Lei dos Nós
a)
Lei dos Nós
![]() b)
Lei das Malhas
b)
Lei das Malhas
Neste circuito tem-se três malhas, são elas; abef, acdf e bcde. Consequentemente pode-se construir três equações. Veremos a seguir que apenas duas delas serão independentes. Uma das equações poderá ser escrita como combinação linear das duas outras. De forma similar ao caso anterior, podemos dizer que se existem M malhas, então existirão M-1 equações linearmente independentes. Veja as equações a seguir;
iii) ![]() malha (abef)
(4a)
malha (abef)
(4a)
iv) ![]() malha (bcde)
(4b)
malha (bcde)
(4b)
v) ![]() malha (acdf)
(4c)
malha (acdf)
(4c)
A dependência linear das equações acima pode ser facilmente verificada, somando as equações iii) e iv) para obter v).
Finalmente a solução final para as correntes é dada resolvendo o sistema de três equações com três incógnitas. Neste caso, podemos usar as equações (i), (iii) e (iv) para construir o sistema de equações. Este sistema pode ser resolvido por qualquer técnica, todas elas levam à mesma solução para as correntes. Neste caso, a solução é dada pelas seguintes equações;
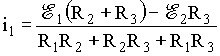 (5a)
(5a)
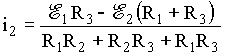 (5b)
(5b)
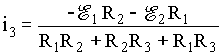 (5c)
(5c)
![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Aug/24/99
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Register No 169.766 -
Biblioteca Nacional - Ministério da Cultura