FEM

Dissipação de Calor em Resitores

Voltar à página principal

Leis de Kirchhoff

Força Eletromotriz (fem )

        Se desejamos estabelecer uma corrente elétrica sobre um resistor R, devemos criar uma diferença de potencial entre os terminais de R. Um modo simples de se produzir tal efeito, seria conectar um dos terminais de R em uma esfera condutora descarregada e o outro terminal, em uma segunda esfera carregada negativamente. O problema principal deste procedimento é que a corrente ou fluxo de elétrons, de uma esfera para outra, será muito rápido, fazendo com que ambas esferas fiquem a um mesmo potencial.
        Para manter uma corrente elétrica por um tempo mais longo, precisamos de ter uma "bomba de carga", isto é um aparelho que mantenha os terminais do resistor sob uma diferença de potencial V. Estes dispositivos, são chamados por fontes ou força eletromotrizes (fem) e um dos mais comums é a bateria, veja Fig.1.
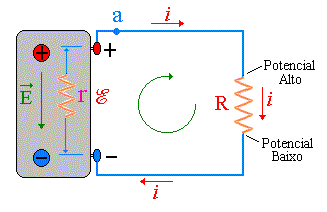
        Discutiremos, agora, dois modos equivalentes de calcular a corrente em um circuito simples como o da Fig.1. Um destes métodos é baseado na conservação da energia e o outro no conceito de diferença de potencial elétrico. O circuito da Fig., contendo uma única malha, consiste apenas de uma bateria (fem ) e uma resistência R, os quais estão conectados por fios condutores e sem resistência. No caso real as baterias têm uma resistência interna, representada aqui pela letra r.

Fig. 1 Força eletromotriz em um circuito elétrico

- Método 1 : Conservação da Energia

O processo de criação de uma corrente elétrica em um condutor, por aplicação de uma diferença de potencial entre os seus terminais, implica na realização de um trabalho para mover cada elétron na presença do campo elétrico E. Este trabalho é igual a;

. (1)

Usando o princípio da conservação de energia, o trabalho realizado pela bateria deve ser igual a energia térmica dissipada no resistor, então:

(2)

onde R_e = R + r é a resistência equivalente do circuito. A equação (2) pode ser reescrita por;

, (3)

isto significa que, no processo de transferência provocado pela bateria, a fem pode ser definida em termos da energia por unidade de carga. A quantidade Ri é a energia usado na movimentação das cargas no interior do condutor.

- Método 2 : Diferença de Potencial Elétrico

Calcularemos agora a soma algébrica da diferença de potencial entre pontos distintos do circuito elétrico na Fig.1. Para isto, percorreremos o circuito no sentido horário (ou anti-horário) partindo do ponto "a" e retornando a este ponto no final do percurso. Assumiremos que o potencial elétrico só pode ter um único valor em cada ponto do circuito, para um dado instante de tempo. Se escolhemos um ponto de partida neste circuito e o percorremos em um dos dois sentidos, horário ou anti-horário, somando algebricamente as variações de potencial encontradas no caminho. Ao voltar ao ponto de partida devemos encontrar o mesmo valor do potencial, isto é, a variação total de V deve ser igual a zero. Em outras palavras podemos dizer que:

A soma algébrica das variações do potencial elétrico encontrados ao longo de um percurso completo, deve ser igual a zero.

Esta regra é conhecida como Segunda Lei de Kirchhoff ouLei das Malhas.

Imaginemos um percurso, realizado no sentido horário, sobre o circuito da Fig. 1, como discutido acima. O ponto de partida pode ser um ponto qualquer, como por exemplo o ponto "a", onde o potencial é V_a. Ao atravessarmos o resistor, notamos uma variação no potencial igual -iR, onde o sinal negativo indica que o potencial extremo superior é maior do que o potencial no extremo inferior. Isso decorre simplesmente do fato de que portadores de cargas positivas movem-se espontaneamente do potencial mais alto para o potencial mais baixo. Ao atravessarmos a bateria de baixo para cima, há um aumento no potencial igual a +, pois a bateria executa um trabalho positivo, sobre as cargas, levando-as de um potencial mais baixo para um mais alto. Isto significa que a bateria funciona como uma fonte de realimentação energética das partículas carregadas, já que elas perdem energia ao passarem pelos resistores. Como a fonte tem uma resistência interna (r), devemos adicionar uma queda no potencial de -ir. Dai chegamos novamente ao ponto "a" com potencial V_a. Esta soma algébrica é igual a;

(4) ou

(5) Como podemos notar, este resultado é independente do ponto de partida escolhido V_a assim como do sentido de percurso escolhido. Este resultado era esperado, pois os dois métodos usados na descrição do circuito estão intimamente ligados à conservação de energia, pois o conceito de diferença de potencial é definido em termos do trabalho realizado para transportar partículas na presença de campo elétrico.

Voltar à página principal

Voltar ao início desta página