|
Energia nos Capacitores |
Voltar à página principal |
Resistores em Série e Paralelo |
|
Energia nos Capacitores |
Voltar à página principal |
Resistores em Série e Paralelo |
Nos capítulos anteriores estudamos as leis e teorias envolvidas com a eletrostática, isto é com a carga em repouso. Neste capítulo começaremos nossos estudos dos fenômenos relacionados com a carga em movimento. Até o ano de 1800 os desenvolvimentos técnicos da eletricidade consistia meramente em produzir cargas estáticas por fricção. Alguns experimentos nesta época usam recursos naturais, como por exemplo os raios, para os estudo dos fenômenos eletrostáticos. Em 1752 Franklin realizou o seu famoso experimento produzindo descarga elétrica, em uma arraia (pipa).
Somente, em 1800, aconteceu um evento de grande importância prática: Alessandro Volta (145-1827) inventou a bateria elétrica e com produziu o primeiro fluxo de carga elétrica em um laboratório. Este experimento abriu uma nova era, transformando nossa civilização.
Quando existe um fluxo resultante de carga através de uma área qualquer, dizemos que há uma corrente através desta área. Se um corpo isolado for colocado em um campo eletrostático, as cargas no condutor rearranjam-se de modo a tornar o campo nulo e o potencial constante no seu interior. O movimento das cargas no processo de redistribuição constitui uma corrente transiente de curta duração, que cessa quando o campo no interior do condutor for nulo. Para manter uma corrente contínua precisamos de algum modo, manter uma força sobre as cargas móveis do condutor. Esta força pode ser proveniente por exemplo de um campo eletrostático E. Tal foça é denominada "força de arrastamento".
O movimento de uma partícula carregada livre em um condutor é muito diferente da de uma partícula no espaço vazio. Depois de uma aceleração momentânea, ela sofre uma colisão inelástica com uma das partículas fixas no condutor, perde a velocidade que havia adquirido na direção da força motriz, começando tudo novamente. Assim, ela se move no sentido da força de arrastamento com uma velocidade média chamada de velocidade de arrastamento.
Define-se quantitativamente a corrente através de uma área como a carga resultante que flui desta área por unidade de tempo. Assim, se uma carga resultante dq fluir através de uma área no tempo dt, a corrente i através da mesma será:
(1)
que é uma quantidade escalar. De acordo com esta definição
a corrente elétrica expressa a taxa de variação da
carga em função do tempo. Em outras palavras o valor de i
será uma medida da rapidez com que cargas atravessam uma dada seção
transversal por unidade de tempo.
A unidade de corrente no
MKS é um coulomb por segundo [C/s], que algumas vezes é chamada
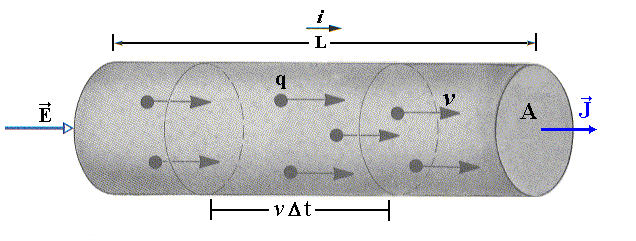
de Ampère [1A]. A corrente através de uma área (Fig.1)
pode ser descrita em termos da velocidade de arrastamento das cargas que
movem em um condutor. Por exemplo a carga dq que flui através de
uma área A, em um condutor cilíndrico, no tempo dt será
igual a;
![]() (2)
(2)
onde N é o número de cargas por unidade de volume e v é a velocidade de arrastamento das cargas.
Em geral se o condutor contiver várias partículas diferentes, com diferentes densidades de cargas, e movendo-se com diferentes velocidades a corrente será;
![]() (3)
(3)
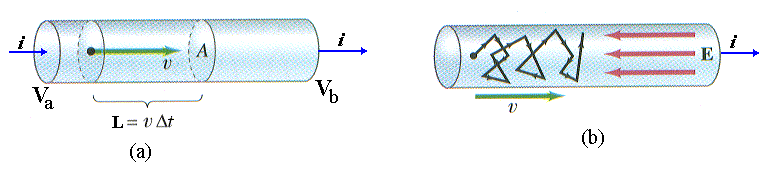
Fig.2 - Movimento de uma carga no interior do
condutor
A corrente por unidade de área transversal é chamada densidade de corrente J, definida por;
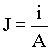 (4)
(4)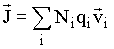 (5)
(5)Podemos generalizar a equação (3) para o caso de cargas fluindo através de uma superfície fechada S qualquer, logo,
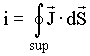 (6)
(6)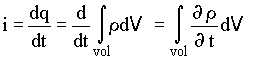 (7)
(7)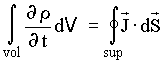 (8)
(8)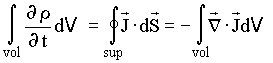 (9)
(9)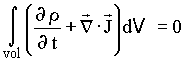 (10)
(10)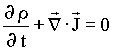 (11)
(11)![]() Electronic
Address : kcmundim@unb.br
Electronic
Address : kcmundim@unb.br
Last Updated: Aug/24/99
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Register No 169.766 -
Biblioteca Nacional - Ministério da Cultura