Circuito LC

Energia Magnética em Circuito RL

Voltar à página principal

Energia em Circuito LC

Circuito LC

A figura abaixo (Fig.1) mostra um circuito do tipo LC. No circuito (a), colocamos a fonte em contato apenas com o capacitor para carregá-lo. Após o carregamento completo do capacitor, desligamos a chave do ponto A e ligamos no ponto B desconectando a fonte do circuito. Mesmo assim o capacitor permanece carregado.

Fig. 1 - (a) Carregando um capacitor. (b) Circuito LC em atividade.

A ligação da chave no ponto B faz com que apareça uma corrente no circuito. Esta corrente passará pelo indutor criando consequentemente campos magnéticos. Isto significa que, parte da energia que estava armazenada no capacitor é transformada em energia magnética no indutor.
A seguir, mostraremos que é possível encontrar uma equação que descreva o comportamento temporal das cargas e correntes no novo circuito. Existem vários métodos para resolver este problema. Um deles seria usar as leis de Kirchhoff como no caso anterior. Neste caso, diferentemente, determinaremos as equações para q e i usando a lei de conservação de energia, como a seguir.

Sabemos que as energias armazenadas num capacitor e num indutor são respectivamente dadas por;

(1)

Como o sistema é fechado e ideal, temos que a energia total (U_T) no circuito é uma constante. Como existem apenas dois elementos no circuito, podemos afirmar que a energia total, deve ser uma soma das energias elétrica (U_E) e magnética (U_B), produzidas no capacitor e no indutor respectivamente. Assim temos que;

(2)

Derivando ambos lados da equação acima em função do tempo temos que;

(3)

ou de uma forma mais simplifica;

(4)

A equação acima é uma equação diferencial de segunda ordem, incompleta e homogênea. Como no caso anterior, existem vários métodos de resolve-la. Analisando a equação diferencial acima notamos que a derivada segunda de q(t) é a própria função q(t), a menos de algumas constantes. Isto sugere, intuitivamente, que a que a solução desta equação diferencial deve ser uma função do tipo seno, cosseno ou combinações delas. Com base nisto assumimos que q(t) em função do tempo seja da forma;

(5)

onde A , w₁ e f são constantes a serem determinadas, usando condições adicionais. Inicialmente, como condição de contorno, assumimos que para o instante t = 0 a carga no capacitor é máxima, isto é q(t=0) = q_o =A e a fase f = 0.
Substituindo esta equação para q(t) na equação diferencial acima, podemos facilmente verificar que q(t) é uma solução para (16). Isto é;

(6)

. (7)

Isto implica a constante w₁ pode ser determinada. Neste caso podemos dividir ambos lados da equação por
Lq_ocos(w₁t+f ) o implica em;

. (8)

Observamos com isto que w₁ deve ser a freqüência angular de oscilação do circuito. A freqüência angular depende apenas da indutância e capacitância do circuito LC. Como a carga do circuito é variável no tempo consequentemente a corrente será também dependente do tempo.

Para verificar esta afirmação, basta derivar a equação (17) em função de t. Isto é;

(9)

A figura abaixo são os gráficos para a corrente e a carga variando no tempo.

Fig. 2 - Comportamento da carga e corrente em função do tempo

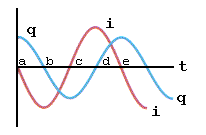
A simulação a seguir mostra o funcionamento de um circuito LC ideal em funcionamento. Note que inicialmente o capacitor é carregado eletricamente pela bateria. Em seguida liga-se o capacitor ao indutor. A partir deste instante o circuito passa a oscilar indefinidamente, transformando energia elétrica em magnética e vice-versa. Observe que não há perda de energia no circuito LC ideal, pois ele não tem resistência elétrica. No capacitor a energia fica armazenada em termos de campos elétricos e no indutor em termos campos magnéticos.

É importante ressaltar que a energia total no sistema é constante e portanto não variável no tempo. Este é um fato curioso pois a energia total é uma soma das energias elétricas e magnéticas, as quais são variáveis no tempo. Então, podemos colocar a seguinte questão: Como pode a soma de duas grandezas (energias elétrica e magnética) variáveis no tempo ser um grandeza constante e não dependente do tempo ?

A simulação abaixo, descreve o comportamento oscilante de um circuito LC. Observe que ele oscilará indefinidademente, transformando energia elétrica em magnética e vice-versa.

Fig. 3 - Funcionamento de um circuito LC ideal

Voltar à página principal

Voltar ao início desta página