Aula 9

Introdução à Mecânica Quântica

1. A equação de Schrödinger

            Nas seções anteriores mostramos a necessidade de se construir uma nova mecânica para os sistemas atômicos e moleculares, para os quais a teoria de Newton ou mecânica Newtoniana não se aplicava. Devido a fatos tais como, a quantização da radiação emitida por um corpo negro, a quantização do átomo de Bohr, a dualidade onda corpúsculo tanto para a luz quanto para o elétron, assim como o princípio da incerteza de Heizenberg a nova mecânica deveria ter uma formulação compatível com estes fatos. A primeira formulação para esta nova teoria foi proposta pelo físico austríaco Erwin Schrödinger em 1926. De acordo com Schrödinger devido a dualidade onda-corpúsculo da matéria, mesmo que uma partícula se mova em uma trajetória definida ela estará distribuída em todo o espaço como uma onda. Neste sentido, uma onda na nova mecânica (mecânica quântica) equivaleria ao conceito de trajetória na mecânica clássica e seria representada por uma função denominada função de onda, y (psi).
            Nesta mesma época Schrödinger propôs uma equação diferencial, nas coordenadas espaciais e no tempo cuja solução era a função de onda. Esta equação ficou conhecida como equação de Schrödinger, que para uma partícula de massa m se movendo em uma dimensão e sob a ação de um potencial V(x) tem a seguinte forma;

 

                                                              (1)

Leia aqui o artigo original de Schrödinger.

            No caso de um movimento tri-dimensional tem-se que;

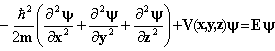                                          (2)

ou

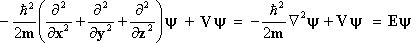              (3)

onde o operador diferencial  é denominado por Laplaciano.

Se o movimento da partícula é dependente do tempo a equação de Schrödinger assume a forma;

                                                           (4)

ou de forma simplificada,

                                                                                 (5)

O operador H é denominado de operador Hamiltoniano. Observe, na equação de Schrödinger, que a energia (uma observável física) é representada por um operador diferencial.
 

2. Soluções da Equação de Schrödinger

            Vimos que a equação de Schrödinger é uma equação diferencial cuja solução é uma função de onda. No caso de uma partícula de massa m se movendo em uma dimensão e sobre a ação de um potencial constante (V) a equação de Schrödinger tem a forma;

               (6)

Sendo o potencial constante uma possível solução para esta equação, a qual pode ser obtida por diferentes métodos dentro da teoria das equações diferenciais, é da forma, ;

                                                          (7)

onde i é um número complexo imaginário. Vemos com isto que a solução da equação de Schrödinger é uma função de onda complexa. Como y é uma função complexa (imaginária) ela não deve ter significado físico e, portanto não pode ser medida em laboratório. Apenas as grandezas ou observáveis reais têm significado físico e podem ser medidas em laboratório. O módulo da função de onda ao quadrado  é uma grandeza não complexa, portanto ele deve ter significado físico que, de acordo com Max Born,  mede a probabilidade de se encontrar uma partícula na região do espaço delimitada pelo elemento de volume  t  e  t +dt.

            Pode-se mostrar que existem outras soluções mais gerais para a equação de Schrödinger acima. Uma dessas soluções é a função formada por combinações lineares de funções complexas;

                                                               (8)

Esta equação é uma combinação linear de duas ondas planas que se propagam em uma dimensão nas direções +x e –x. A e B são constantes representando as amplitudes de cada uma das ondas.

            Para verificar se realmente esta função (eq.8) é solução da equação de onda, vamos aplicá-la na equação de Schrödinger para resolver o problema de uma partícula livre, e com isto calcular a energia total do sistema. Se a função de onda y é expressa como uma combinação linear de ondas planas como a seguir,

   ,

pode-se determinar a energia do sistema resolvendo a equação de Schrödinger, isto é,

                                                                          (9)

Caso de uma Partícula Livre

      No caso de uma partícula livre temos que o operador energia, ou operador Hamiltoniano  é descrito pela derivada segunda da função onda em relação à coordenada x,

                                             (10)

Neste caso V(x) = 0, já que a partícula é livre e, portanto ela não está sobre a ação de qualquer tipo de potencial externo. Substituindo a equação (8) em (10) temos que;

    (11)

 

 e

Substituindo estes dois resultados na equação (7) temos que,

           (12)

reordenando o lado direito da equação acima, temos que;

                    (13)

que pode ser rescrita por,

A equação (13) é exatamente igual a equação (10), mostrando assim que a função de onda (eq. 8) é uma autofunção do operador Hamiltoniano para uma partícula livre, cujo valor da energia é igual a;

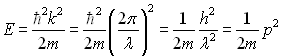                                                                                             (14)

onde k é o número de ondas.
 
 

    O conteúdo desta página está em constante atualização.
Correções no texto esugestões serão bem vindas.

Electronic Address :  kcmundin@unb.br
Last Updated: Fev/17/2002
Copyright 1997: Kleber C. Mundim. All rights reserved.
Register N^o  169.766 - Biblioteca Nacional - Ministério da Cultura
phone: 55 61 3307 2966     FAX 55 61 3273-4149