Aula-7

-  A Mecânica Ondulatória e o Significado de Y
-  Princípio da Incerteza de Heisenberg
 
 

2-  A Mecânica Ondulatória e o Significado de Y

        Vimos que com as observações experimentais sobre o efeito de interferência no caso da matéria, assim como da luz, tornou-se claro que ambas, matéria e radiação, têm comportamento ondulatório. Por outro lado, o efeito fotoelétrico indica que a luz se comporta como uma coleção de partículas viajando como velocidade c = 300.000 km/s. Estas partículas foram chamadas de fótons. Sabemos também, que os elétrons comportam-se como se fossem partículas, mesmo sabendo que eles podem produzir também efeitos de interferência. Como podemos reconciliar este aparente conflito ? Isto é, tanto a matéria quanto a luz têm comportamentos duais onda-corpúsculo ?
        Em 1926, Max Born sugeriu uma unificação pictórica para estes conceitos introduzindo o significado de amplitude de onda de matéria.

Max Born

    Primeiro, vamos lembrar que a densidade de energia de uma onda eletromagnética, ou energia por unidade de volume, é proporcional ao quadrado de sua amplitude (A² ) . Isto pode ser demonstrado usando as equações de Maxwell para o eletromagnetismo (veja apêndices 1 a 3). Isto significa que;

 Levando em conta o comportamento corpuscular da luz (fóton), a energia total é igual a E = n(hn), onde n é a freqüência da luz e n é o número de fótons. Dai tiramos que;

    Das duas últimas equações vemos que o número de fótons por unidade de volume é proporcional ao quadrado da amplitude da radiação eletromagnética. Isto é,

Isto levou Born assumir que a onda de matéria, representada pela função Y(x,t),  tem uma amplitude tal que o seu quadrado é igual ao número de partículas por unidade de volume,  isto é,

Esta conexão, tanto para as radiações eletromagnéticas quando para as ondas de matéria, produzia um casamento perfeito entre os conceitos onda e partícula.

       Para entender um pouco dessas perturbações vamos estudar um problema simples, unidimensional, dado pelos movimentos possíveis de uma partícula de massa m situada entre paredes rígidas, separadas entre si por uma distância d, como se vê na Fig.1. A função de onda pode ser obtida por analogia com um problema conhecido de Mecânica, os dos modos naturais de vibração de uma corda de comprimento d, fixa nas extremidades, como mostra a Fig.1.

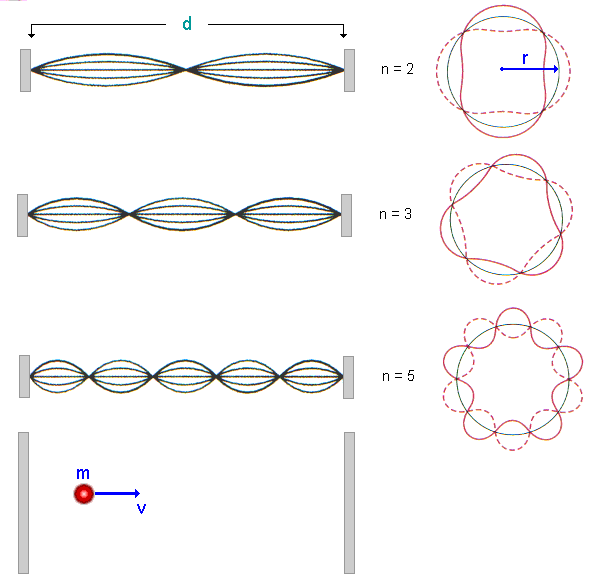
Fig.1 - Ondas Estacionárias

As condições de contorno para uma corda vibrante impõem que em cada extremidade, haja um nó. Isso significa que o comprimento de onda l deve ser escolhido de tal forma que

o que implica na quantização do comprimento de onda l.   Equivalentemente, a perturbação ondulatória de uma corda é representada por uma onda estacionária, cuja dependência espacial e temporal é igual a Asen(kx-wt), onde A é uma constante e k = 2p /l é o número de onda. Visto que l é quantizado, k também deverá ser, isto é,

o que nos leva a seguinte função de onda,

                                                                              (1)

Examinando-se a equação anterior para t = 0, conclui-se que, qualquer que seja o valor de n, existirão sempre nós em x = 0 e x = d, como as condições de contorno o exigem.

    Considere-se agora uma partícula confinada entre duas paredes rígidas. Como as paredes são supostas perfeitamente rígidas, a partícula não pode penetrar nelas, e portanto, Y , que de alguma forma representa o movimento da partícula, deve anular-se para x = 0 e x = d. Os comprimentos de onda permitidos para as ondas de matéria devem ser dados por l =2d/n. Substituindo l por h/p, tem-se

,

o que mostra que o momento linear da partícula é quantizado. De acordo com a mecânica Newtoniana o momento linear p (=mv) pode ser relacionado com a energia E ( que é inteiramente cinética e igual, portanto, a mv²/2) pela expressão

  .

Combinando entre si as duas equações anteriores, obtém-se a condição de quantização da energia E, a saber,

        Dai conclui-se que a partícula não pode ter uma energia qualquer, como seria de se esperar classicamente, mas apenas valores  discretos. Dessa forma a onda de matéria pode ser descrita, em estrita analogia com a equação (1) para o caso de uma onda em mecânica em cordas, isto é,

onde a amplitude  A = Y_o .
    A Fig.2, pode servir, igualmente, para mostrar como variam dentro da caixa, as amplitudes das ondas estacionárias para os estados de movimento correspondentes a n = 1, 2 e 3. Vê-se claramente, neste problema, como o fato de se localizar ou confinar uma partícula provoca a quantização de sua energia.

      Simulação de uma difração de elétrons por fendas

    Max Born foi o primeiro a sugerir que o valor da grandeza Y² em um ponto qualquer exprime a probabilidade da partícula estar próxima desse ponto. Mais exatamente, considerando-se um elemento de volume dV que contenha esse ponto, a probabilidade da partícula ser ai encontrada, num dado instante, é dada por Y²dV. Esta interpretação de Y fornece uma conexão estatística entre a partícula e onda a ela associada; diz-nos onde a partícula provavelmente estará e não onde de fato está.

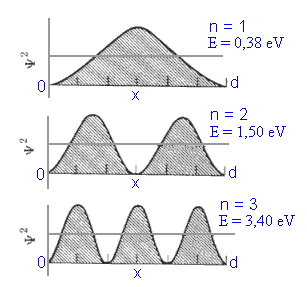
Fig.2   - Representação da função de probabilidade Y²

No caso de uma partícula confinada entre paredes rígidas, a probabilidade de se achar a mesma entre dois planos situados a distância x e x+dx de uma das paredes, num instante t =0,  (ver Fig.2) é dada por

Logo, a densidade de probabilidade é dada por

        A idéia de estados estacionários dos átomos corresponderem a ondas estacionárias de matéria foi usada por Erwin Schrödinger, em 1926, como base da Mecânica Quântica Ondulatória, que é uma das várias formulações equivalentes da Física Quântica. Uma importante grandeza na Mecânica Ondulatória é a função de onda Y , que mede a perturbação ondulatória das ondas de matéria. Equivalentemente, no caso das ondas produzidas em cordas, a perturbação ondulatória pode ser avaliada pela elongação y; no caso das ondas sonoras pela variação da pressão e no caso das ondas eletromagnéticas pelo vetor campo elétrico E.

E. Schrödinger

        Com a equação de onda tridimensional proposta por Schrödinger, o problema do átomo de hidrogênio, assim como as questões relacionadas com a velha teoria atômica de Bohr, foram corretamente resolvidas. A equação de onda de Schrödinger é uma equação diferencial nas variáveis espaciais e temporal, como veremos nas próximas seções.
 

3-    Princípio da Incerteza de Heisenberg
 

        Alguns físicos acreditam que apenas as grandezas suscetíveis de medida têm significado real em Física. Só se conseguisse focalizar um super microscópio em um elétron, no interior de um átomo, e se pudesse "vê-lo" percorrendo a sua órbita, seria lícito declarar que esta órbita teria significado. Entretanto, mostraremos a seguir que é fundamentalmente impossível efetuar uma observação desse tipo, mesmo com qualquer instrumento ideal que se possa conceber. Em conseqüência, afirma-se que essas órbitas atômicas não têm significado físico.

        Vê-se a Lua, enquanto percorre a sua órbita em torno da Terra, devido à luz solar que ela reflete na nossa direção. Ora, a luz transfere momento linear ao objeto pelo qual é refletida. Em princípio, essa luz refletida perturbaria o movimento da Lua em sua órbita, embora um raciocínio simples, mostre que esse efeito é desprezível. Em se tratando de elétrons, a situação é bastante diferente. Isto significa que ao incidir luz sobre o elétron, no sentido de localizá-lo observando a luz refletida, o elétron sofrerá um recuo alterando completamente seu movimento de modo que não pode ser evitado, ou mesmo corrigido. Esta incapacidade intrínseca de descrever os movimentos do elétron, de modo clássico, é expressa pelo princípio da incerteza de Heisenberg. Para formular esse princípio, considere-se um feixe de elétrons mono energéticos, de velocidade v, deslocando-se da esquerda para a direita na Fig.3. Com este experimento procura-se determinar a posição de um certo elétron de ordenada y e de velocidade v_y . Caso se consiga medir essas grandezas com precisão ilimitada, poder-se-á afirmar ter-se estabelecido exatamente a posição e o movimento do elétron. Entretanto, ver-se-á ser impossível efetuar simultaneamente as duas medidas citadas com precisão ilimitada.

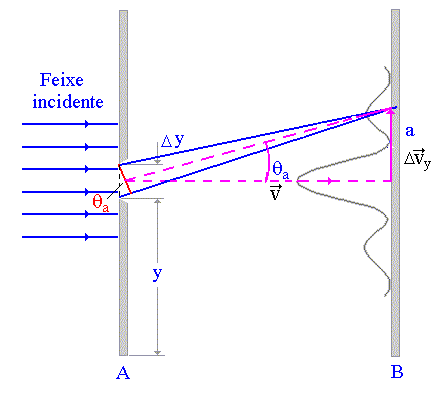
Fig.3       Difração de uma partícula

        Como o elétron pode comportar-se como uma onda, o mesmo sofrerá difração ao atravessar a fenda e, colocando-se uma chapa fotográfica em B (Fig. 3), obter-se-á uma figura de interferência por difração típica. A existência dessa figura de difração significa que existe uma incerteza nos valores das velocidades v_y dos elétrons que ultrapassaram a fenda.

        Seja v_ya o valor de v_y correspondente a uma elétron que atinge o primeiro mínimo do anteparo, indicado pelo ponto a e definido por um ângulo característico q_a. Considera-se v_ya como uma medida aproximada da incerteza Dv_y  relativa ao valor da velocidade v_y dos elétrons emergentes da fenda.

        Sabemos da difração, em fenda única, que a condição de mínimo ou interferência destrutiva, no espectro de difração é dada pela equação

O primeiro mínimo da figura de difração é dado pela seguinte equação acima, no caso m = 1

para q_a suficientemente pequeno. Para atingir o ponto a, v_ya (= Dv_y) deve ser tal que

  .

Combinando as duas equações anteriores obtemos que

Ora, o comprimento de onda l do feixe de elétrons é dado por h/p ou h/mv; substituindo o seu valor na equação anterior, vem que

  ,

que pode ser reescrita por

onde Dp_y = mDv_y é a incerteza no conhecimento sobre o momento dos elétrons; Dy é incerteza no conhecimento sobre a sua ordenada (ou posição). A equação acima assegura que, como o produto dessas incertezas é constante, não se poderá medirp_y e y, simultaneamente com precisão ilimitada. Se quiser melhorar a medida de y usa-se uma fenda mais estreita. Entretanto isso resultará em espectro de difração mais largo. O aumento da largura do espectro de difração significa ter piorado o conhecimento da componente vertical ou, em outras palavras, que Dp_y aumentou. É isso, exatamente, o que prevê o princípio de Heisenberg.

    As limitações nos valores das precisões das medidas impostas pelo princípio de Heisenberg, nada têm a ver com as imperfeições dos aparelhos de medida. Pode-se até postular a existência dos mais perfeitos equipamentos de medida concebível. O princípio de Heisenberg representa uma limitação fundamental, imposta pela Natureza.

W. Heisenberg

Num caso mais geral deste princípio pode se afirmar que

    A constante de Planck, h, provavelmente não aparece em qualquer outra fórmula com um significado mais profundo do que nas equações acima. Se o aludido produto fosse igual a zero, em vez de h, estariam corretas as noções clássicas sobre partículas e órbitas.

   Exemplo

        Um elétron, forçado a se mover em uma dimensão, tem uma incerteza de posição = 1,0x10^-8 metro. Determine a incerteza mínima em sua velocidade escalar. Ache a incerteza correspondente para uma bola de 2 kg confinada do mesmo modo.

Solução:
        De acordo com o princípio da incerteza de Heisenberg, temos que,

ou

Para o elétron isto implica uma incerteza de velocidade

Enquanto que para a bola de 2 kg,

Disto, vemos muito claramente que a limitação que a relação de incerteza impõe a corpos microscópicos é muito mais significativa do que aquela que resulta no caso de objetos macroscópicos.
 
 
 

    O conteúdo desta página está em constante atualização.
Correções no texto e sugestões serão bem vindas.

Electronic Address :  kcmundim@unb.br
Last Updated: Sep/12/2000
Copyright 1997: Kleber C. Mundim. All rights reserved.
Register N^o  169.766 - Biblioteca Nacional - Ministério da Cultura
phone: 55 61 3307-2966