Aula-6

- Átomo de Hidrogênio
- Princípio da Correspondência
- Estrutura Atômica e Ondas de Estacionárias (Postulado de De Broglie)

1- Átomo de Hidrogênio

A radiação emitida por qualquer fonte de luz pode ser estudada para determinar que tipo comprimentos de onda ou freqüências estão presentes neste sistema. Por exemplo, uma lâmpada incandescente exibe um espectro contínuo de radiação. Por outro lado, muitas outras fontes de luz emitem apenas em algumas freqüências bem definidas denominadas por "linhas espectrais". Em particular observa-se que um gás de hidrogênio emite radiações em um espectro reduzido e limitado. A seguir discutiremos o espectro de emissão do hidrogênio que é o sistema atômico mais elementar conhecido.
Antes do desenvolvimento da teoria quântica, esses complicados espectros de linha foram tomados como evidência de uma estrutura interna mais envolvida por átomos. Acreditava-se então que os átomos tinham muitos modos possíveis de oscilações, como cordas de violinos ou tubos de órgãos, e que a excitação destes modos davam origem à radiação correspondente às suas freqüências individuais. Até 1885, 14 linhas espectrais de hidrogênio tinham sido identificadas e seus comprimentos de onda precisamente medidos. Johann Balmer então conseguiu achar uma expressão matemática empírica que descreveu precisamente todos estes comprimentos de ondas conhecidos. Ele achou que as séries observadas de comprimentos de onda espectrais poderiam ser espressa por

Balmer n = 3, 4, 5 .....

onde n se supôs serem valores inteiros, isto é, n = 3,4,5,6,..... e R é uma constante que agora é denominada de constante de Rydberg. Na época o valor desta constante era de

Em seguida outras séries espectrais foram determinas teoricamente com base na expressão de Balmer. A primeira delas foi apresentada por Paschen (1908) usando a relação;

Paschen n = 4, 5, 6 .....

Em seguida vieram as séries de Lyman e Brackett, as quais referiam a região do infravermelho e ultravioleta do espectro de emissão do gás de hidrogênio, respectivamente. Estes espectros podem ser descrito pelas equações de Balmer modificada,

Lyman n = 2, 3, 4 .....

Brackett n = 5, 6, 7 .....

Assim determinou-se, empiricamente, que os espectros de linhas distintos emitidos pelo hidrogênio poderiam ser ajustados pela relação de Balmer generalizada;

n > m

onde m e n são números inteiros. Como é positivo, os inteiros m e n devem satisfazer a desigualdade m < n.
A Fig. 1 mostra as séries espectrais conhecidas e descritas pela regra de Balmer.

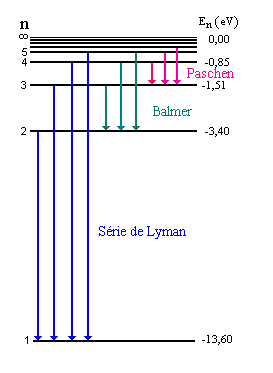
Fig-1 Diagrama de níveis de energia do hidrogênio:
transições de Paschen, Balmer e Lyman.

Investigações do espectro de hidrogênio levaram Niels Bohr a postular que as órbitas circulares dos elétrons (Fig. 2) fossem quantizadas, ou seja, que os seus momentos angulares pudessem assumir apenas múltiplos inteiros de um certo valor básico. Bohr propôs um modelo de átomo de hidrogênio, com notável sucesso no cálculo dos comprimentos de onda das linhas do espectro conhecido do hidrogênio e na previsão das linhas do espectro nas regiões do infravermelhos e do ultravioleta.

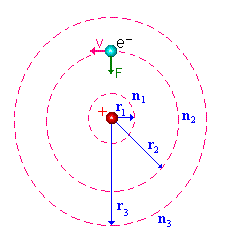
Fig.2 -Átomo de Bohr: órbitas circulares e estáveis.
Os raios estáveis são dados por r_n= n²r_o

A simulação abaixo ilustra o processo de absorção e emissão de fótons por uma átomo. Observe que inicialmente o elétron se localiza no nível de mais baixa energia (estado fundamental) e em seguida absorve a energia de um fóton o que promove a transição para um nível de energia superior. Como este novo estado energético não é o de mais baixa energia o elétron volta ao nível inferior, emitindo para isto um fóton com energia igual à que ele recebeu inicialmente.

Absorção e Emissão de Radiação por Átomo

Esta simulação ilustra o processo de absorção e emissão de fótons por uma átomo

A seguir discutiremos as idéias de Bohr. Esse modelo, embora deficiente sob diversos pormenores, ilustra as idéias da quantização dentro da moldura matemática mais simples da Física Clássica. As teorias clássicas vigentes na época e usadas na descrição das órbitas eletrônicas eram incapazes de explicar os espectro do átomo de hidrogênio. Usando a idéia dos osciladores de Planck, Bohr propôs um modelo que explicasse o espectro do átomo de hidrogênio. De acordo com Bohr, neste átomo, só existem estados estacionários, nos quais não há irradiação, mesmo que os elétrons estejam em movimento. A irradiação só aparece quando o átomo efetua uma mudança de um dado estado, de energia E_k, para outro de menor energia E_j. Matematicamente podemos equacionar esta hipótese por,

onde hn é o quantum de energia associado ao fóton que é emitido pelo átomo durante a processo de emissão de luz. Para saber as freqüência permitidas, na equação de Bohr será necessário conhecer as energias dos diversos estados estacionários em que um átomo de hidrogênio pode existir. Esse cálculo foi efetuado, pela primeira vez, por Bohr baseando-se em um modelo específico do átomo de hidrogênio por ele imaginado. O modelo de Bohr teve sucesso apenas no caso do átomo de hidrogênio, mas mesmo assim influenciou muito o desenvolvimento posterior na Física Quântica.

Suponha-se que o elétron do átomo de hidrogênio percorra uma órbita circular de raio r, concêntrica com o núcleo. Admita-se, ainda, que o núcleo, que consiste de um único próton que tenha uma massa muito superior à do elétron. Neste caso, pode-se considerar que o centro de massa do átomo esteja em cima do núcleo. Usando as leis de Newton, podemos escrever algumas equações relacionadas ao movimento do elétron em torno do núcleo, como por exemplo;

Para o elétron ficar fixo na órbita é necessário que as forças centrípeta e coulombiana sejam iguais;

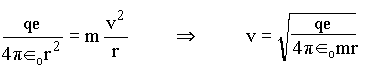
onde q é a carga do núcleo, e é a carga do elétron e v é a velocidade do elétron em torno do núcleo. Com isto podemos calcular as energias cinética e potencial do elétron, por

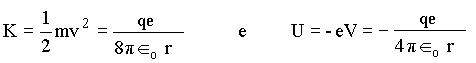
onde r é o raio da órbita do elétron e Î_o a constante dielétrica. Dessa forma a energia total é igual a

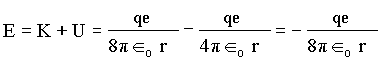
Percebemos que estas grandezas são todas dependentes de r, então se quantizarmos r, conseqüentemente a energia será quantizada. Vamos escrever outras equações, para este problema, que também dependem de r.

Como por exemplo a freqüência, o momento linear e o momento angular, respectivamente

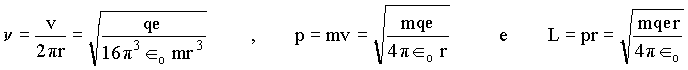
Portanto, conhecendo-se r, todos parâmetros parâmetros da órbita, discutidos acima serão determinados. Até este estágio, Bohr não dispunha de regras que o orientassem, de modo que foi forçado a fazer a hipótese de quantização do momento angular, isto é, o momento angular deveria ser igual a um múltiplo inteiro da constante de Planck dividida por 2p . Assim,

onde n é um número inteiro ou um número quântico. Combinando esta equação com a equação anterior para o momento angular percebemos que r será quantizado,

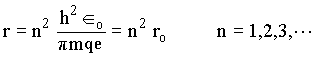
Onde r_o é o raio de Bohr. Substituindo r na equação para a energia total temos que,

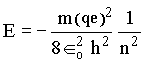
O sinal menos indica que é necessário ceder energia ao átomo para fazer a transição eletrônico para niveis superiores.

Com isto podemos determinar os valores das energias dos estados estacionários permitidos. A Fig. 2, mostra o diagrama de níveis de energias para o átomo de hidrogênio, levando em conta a hipótese de Bohr. Podemos perceber que a medida que n cresce tendendo ao infinito, os níveis de energia se aglomeram, isto é as distância entre eles diminui.

Procedendo de forma análoga ao que fizemos na quantização da energia podemos encontrar uma equação para a freqüência em termos do número quântico n;

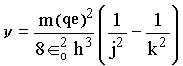
sendo k e j números inteiros, os quais descrevem duas órbitas consecutivas.

Para um elétron passar de um nível para outro ele deve emitir ou receber energia em quantidade bem determinada, isto é receber um quantum de energia.

Sejam por exemplo dois níveis eletrônicos k e j, sendo j superior a k, então a diferença de energia para ir de j até k o átomo deve emitir energia na forma de luz cuja freqüência pode ser determinada calculando a diferença de energia entre os dois níveis, como a seguir

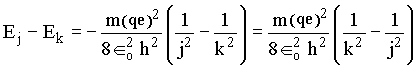
se k = 1 e j = 2, temos que

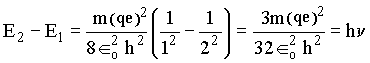
Assim a freqüência da radiação associada no processo de transição de um nível para o outro é igual a,

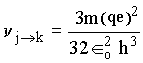
Analisando a equação para a diferença de energia juntamente com a Fig. 2, notamos que para níveis altos ou n grande, o espaçamento entre eles passa a ser quase um contínuo. Este limite seria, em princípio, um dos limites entre a teorias clássica e quântica. Pode se mostrar matematicamente, usando a equação para diferença de energia, que para n no infinito temos um contínuo na separação entre os níveis. Este limite é conhecido como o princípio da correspondência, o qual será discutido na próxima seção.

2 Princípio da Correspondência

Embora todas as teorias da Física tenham suas limitações, geralmente não perdem a validade abruptamente, mas sim de uma maneira contínua, dando resultados que concordam cada vez menos com a experiência. É assim que as previsões da Mecânica Newtoniana se vão tornando menos precisas, à medida que a velocidade de um dado objeto tende a da luz. Uma correlação semelhante deve existir entre as Físicas Quântica e Clássica; resta achar as circunstância sob as quais a última passa a constituir um caso especial da primeira.

O raio da órbita do átomo de hidrogênio, correspondente ao estado de mais baixa energia (chamado estado fundamental), é obtido fazendo-se n = 1 na equação para o raio quantizado e vale r = 5,3x10^-11. Para n = 10.000, entretanto, o raio tornar-se-á (10.000)² vezes maior, ou seja 5,3mm. A este nível de separação espera-se que as freqüências calculadas tanto pela teoria quântica quanto pela teoria clássica devem ser praticamente iguais. Isto significa que os resultados deverão ser diferentes para números quânticos pequenos e concordarem para números quânticos grandes. O fato da Física Quântica se reduzir à Física Clássica, para números quânticos muito grandes, é denominado Princípio da Correspondência, o qual foi proposto por Niels Bohr no início do desenvolvimento da física moderna.

A seguir faremos algumas comparações para as freqüências clássicas e quânticas no caso de números quânticos grandes. As freqüências clássicas e quânticas são dadas por;

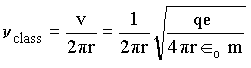
para uma órbita n, temos que

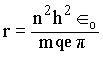
Daí tiramos que a freqüência clássica,

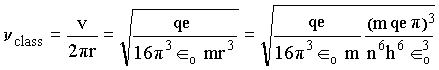
ou de forma simplificada

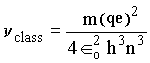
No caso quântico a freqüência é dada pela a diferença de energia,

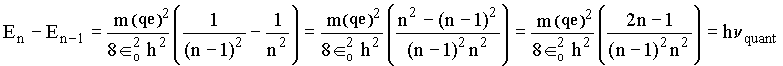
para n grande (n ® ¥ ) temos as seguintes aproximações : 2n-1 » 2n e n –1 » n. Assim a freqüência quântica vem dada por,

Comparando os resultados obtidos para as freqüências clássicas e quânticas concluímos que elas são iguais, no caso de números quânticos grandes, confirmando assim o Princípio da Correspondência de Bohr.

3- Estrutura Atômica e Ondas Estacionárias (Postulado de De Broglie)

O movimento dos elétrons dentro de um feixe não é limitado na direção deste. Pode-se fazer a analogia com uma onda sonora produzida em um tubo longo cheio de gás, com uma onda propagando-se em corda longa, ou ainda com uma onda eletromagnética atravessando um guia de ondas comprido. Todos os quatros casos podem ser descritos por ondas progressivas convenientes e, o que é importante, essas ondas podem propagar-se com qualquer comprimento de onda (dentro de um certo intervalo).

Sejam as últimas três ondas acima limitadas por meio de restrições físicas. No caso das ondas sonoras, isso corresponderia a inserir paredes rígidas nas extremidades de uma seção do tubo, formando uma cavidade acústica ressonante. Para ondas produzidas na corda, consistiria em se remover uma seção finita desta, fixando-a pelas extremidades, como acontece com uma onda em cordas de violino. Quanto às ondas eletromagnéticas, equivaleria a obturar os extremos de um trecho finito de uma guia de ondas, construindo, assim, uma cavidade eletromagnética ressonante. Em conseqüência, vão ocorrer duas mudanças importantes (a) os movimentos passarão a ser representados por ondas estacionárias em vez de ondas progressivas e (b) somente poderão ocorrer certos comprimentos de onda (ou freqüências). Esta quantização do comprimento de onda é um resultado direto de se limitarem ou imporem condições às ondas. É de se esperar que, se os elétrons forem limitados em seus movimentos pelo fato de se encontrarem localizados dentro do átomo, -(a) o movimento do elétron poderá ser representado por uma onda estacionária de matéria e -(b) o movimento do elétron se tornará quantizado, isto é, sua energia poderá ter, apenas, certos valores discretos.

Em 1924, Louis de Broglie, lembrando-se da natureza dualística dos fótons (sugerida por Einstein ao estudar o efeito fotoelétrico), e considerando que todos os fenômenos naturais envolviam certa forma de matéria e de radiação (ondas eletromagnéticas), sugeriu que assim como "as ondas de luz" tinham propriedades de partículas o inverso também deveria ser válido, isto é: " A toda partícula com momento p estaria associada uma onda de comprimento l, isto é : l= h/p, onde h é a constante de Planck e p o momento linear da partícula. Esta relação implicaria que todos os corpos massivos ou partículas, tais como uma bola de bilhar e um elétron, teriam também propriedades de ondas, cujas características seriam regidas pela mesma teoria das radiações.

Com base nesta hipótese de Broglie conseguiu deduzir a condição de quantização (de Bohr) do movimento angular aplicando condições de contorno adequadas às ondas de matéria do átomo de hidrogênio.

Louis de Broglie

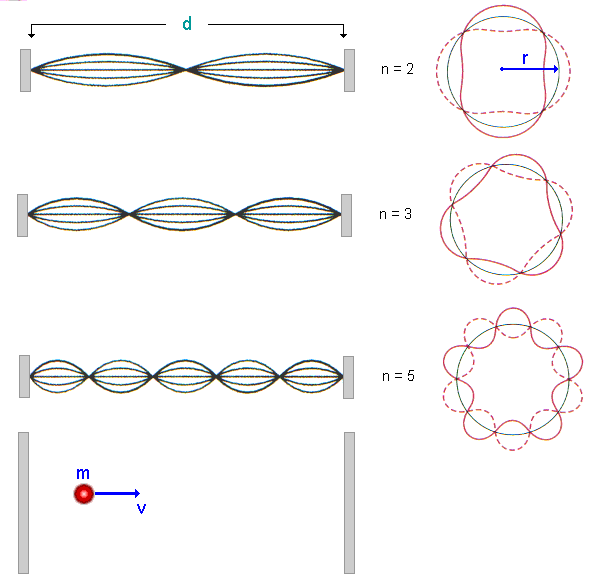
Fig.1 Diferentes tipos de Ondas estacionárias

A Fig.1, apresenta três instantâneos de uma onda estacionária de matéria, associada com uma corda presa nas extremidades e uma órbita de raio r. O comprimento de onda de De Broglie (l = h/p) foi escolhido de tal modo que a órbita de raio r contivesse um número inteiro n de ondas de matéria, ou seja,

Isto dá imediatamente

que é a condição de quantização de L, de acordo com Bohr.

Historicamente é importante ressaltar que quando de Broglie formalizou suas idéias sobre a onda de matéria [publicadas nas Comptes Rendus de l´Academie des Sciences de Paris 177, pgs. 507; 548; 630 (1923); 179, p. 39 (1924)] e apresentou-as, ainda em 1924, como Tese de Doutoramento, intitulada "Recherche sur la Théorie des Quanta", à Faculdade de Ciências da Universidade de Paris (Sorbonne), houve um certo embaraço por parte dos professores que iriam julgá-la, uma vez que essa Tese fugia as cânones tradicionais da Física. Assim, ela foi encaminhada ao físico francês Paul Langevin (1872-1946) para julgamento. De imediato, ele enviou uma cópia ao seu amigo Einstein que, por sua vez, pediu ao físico alemão Max Born (1882-1970) uma opinião séria sobre a mesma, escrevendo-lhe: Leia isto! Embora pareça ter sido escrito por um louco, está escrito corretamente. Quando Einstein devolveu a Tese de d´Broglie a Langevin, disse-lhe que podia aprová-la, já que a mesma continha muitas descobertas importantes. É oportuno destacar que a idéia da “onda de matéria de Broglieana” foi formalizada pelo físico austríaco Erwin Schrödinger (1887-1961), em 1926, por intermédio da célebre Equação de Schrödinger a qual será estuda nas próximas seções.

Leia aqui o artigo original de Loius d´Broglie.

Voltar à página principal Voltar ao início desta página

O conteúdo desta página está em constante atualização.
Correções no texto e sugestões serão bem vindas.