Aula 13
1.
Postulados Básicos da Mecânica
Quântica
Vimos que a mecânica quântica foi introduzida do mesmo modo que a mecânica newtoniana, a teoria cinética, a termodinâmica e a relatividade especial, isto é; a partir de dois postulados, o princípio da incerteza e o princípio da correspondência, constrói-se a mecânica quântica.
A mecânica quântica, em particular, está baseada em cinco postulados; o primeiro deles refere-se a existência de uma função de onda denominada y, o segundo estabelece a equação que governa y, o terceiro e o quarto estabelecem as restrições que devem ser obedecidas pela função y e o quinto estabelece as regras de uso de y na determinação das variáveis dinâmicas em um dado sistema físico, os quais são discutidos abaixo,
Postulado I
Para
cada
partícula de massa m existe uma função de
onda y(x).
Postulado II
Para
uma
partícula de massa m cuja energia total clássica
é constante (E) e cuja energia potencial
é dada por uma função V(x,y,z), a função
de onda
satisfaz a equação de
Schrödinger, dada por;
 (1)
(1)
Postulado III
A função de onda y e sua derivada dy/dx deve ser finita, unicamente determinada e contínua para todos os valores de x.
Postulado IV
A função de onda deve conter informações sobre a localização da partícula, isto é a partícula deve estar em algum lugar do espaço;
![]() (2)
(2)
Postulado V
Se vários experimentos idênticos são realizados para determinar a energia, posição ou o momento de um número grande de sistemas quânticos independentes, a seguinte expressão denominada valor esperado, dá o valor médio das grandezas medidas em todos os sistemas, como por exemplo;
a)-
O valor esperado da energia ![]() é igual a;
é igual a;
![]() (3)
(3)
b)- O valor esperado da posição é dado por;
![]() (4)
(4)
e o valor esperado do quadrado da posição é igual a;
![]() (5)
(5)
c)- O valor esperado do momento é dado por;
![]() (6)
(6)
e o valor esperado do quadro do momento linear é igual a;
![]() (7)
(7)
2. Partícula Confinada em uma Caixa
Um exemplo da aplicação da equação de Schrödinger onde estes postulados são requisitados é o caso de uma partícula de massa m, confinada em uma caixa, com paredes infinitas. A parede da caixa é definida por um potencial V(x) infinito, como mostra a Fig.1.
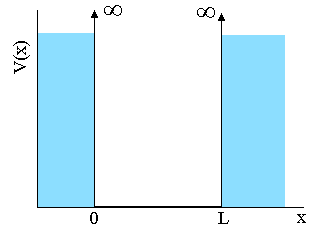
Fig.1 - Potencial com barreiras infinitas
A equação de Schrödinger para a região entre as paredes, isto é no interior da caixa, o potencial é nulo (V(x)=0) que é o mesmo para uma partícula livre. Assim a solução geral para a equação de Schrödinger é igual a uma combinação funções de ondas planas como a seguir;
![]() (8)
(8)
Para verificar se realmente esta função de onda é solução da equação de Schrödinger basta substituí-la na eq (1) e fazer as derivadas. Daí, tira-se que a energia total da partícula (E) é igual a energia cinética, já que a energia potencial (V) é igual a zero no interior da caixa. Isto é;
![]() (9)
(9)
Resolvendo a derivada do lado esquerdo da equação acima tem-se que,
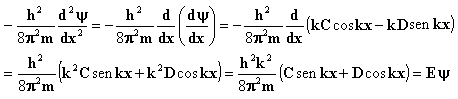 (10)
(10)
de onde tiramos o seguinte valor para a energia,
![]() (11)
(11)
É necessário ressaltar que esta solução deve satisfazer aos postulados básicos da mecânica quântica assim como as condições de contorno do problema em questão. Fisicamente é impossível encontrar a partícula em qualquer região fora da caixa já que o potencial nesta região é infinitamente grande. Neste caso a função deve ser nula nesta região. Isto é,
![]() (12)
(12)
Aplicando a primeira condição de contorno estabelecida na eq. (12), a função de onda (eq.8) deve ter o coeficiente D igual a zero (D = 0), pois sen(0) = 0 e cos(0) = 1, para x = 0. Isto é,
![]() (13)
(13)
Assim, a função de onda fica simplificada por;
![]() (14)
(14)
Aplicando a segunda condição de contorno temos que;
![]() (15)
(15)
a função seno é igual zero sempre que o seu argumento for um múltiplo inteiro de p, isto significa que;
![]() (16)
(16)
O valor de n = 0 é descartado, pois ele implica que a partícula y(x) = 0 em todos os pontos do espaço, o que significa que não se tem nenhuma informação sobre a posição da partícula. Valores negativos de n implicaria apenas na mudança de sinal da função de onda já que a função seno é uma função impar: sen(-x)= -sen(x).
Com base nestas condições de contorno a função de onda assume a seguinte forma;
![]() (17)
(17)
Observamos também, que neste caso, existem vários estados possíveis para a partícula, cujas energias são dadas em função do número quântico n;
![]() (18)
(18)
Vimos assim que as condições de contorno restringem os tipos de funções de ondas que são aceitáveis para este problema especifico. Um resultado muito importante obtido nesta aplicação é que a energia tem valores quantizados como mostra a eq.18 e a Fig.2.
2.1 Sobre a Normalização da Função de Onda
Vimos anteriormente que nem todas as soluções da equação de Schrödinger são autofunções adequadas ao problema em estudo, pois ela deve satisfazer, no mínimo aos postulados da mecânica quântica, discutidos anteriormente. Em particular, ela deve satisfazer ao postulado IV, isto é;
![]() (19)
(19)
Com este postulado foi possível, então determinar o valor da constante C e assim a função de onda assume a seguinte forma;
![]() (20)
(20)
Variando o número quântico n, a função de onda assume as seguintes formas;
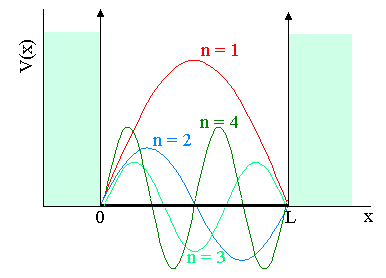
Fig. 2 - Movimento quantizado da partícula
2.2 Sobre a Ortogonalidade da Função de Onda
Vimos anteriormente que a função de onda obtida para o caso de uma partícula confinada em uma caixa e com paredes infinitas, defini vários estados possíveis em que a partícula pode existir. Estes estados podem ser determinados variando o número quântico n. Um fato interessante é que estes estados são descritos por funções ortogonais, isto é;
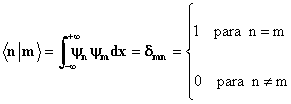 (21)
(21)
Que em particular para os estados n = 1 e m = 3, tem-se que
![]() (22)
(22)
Cujo caso geral é dado pela seguinte equação;
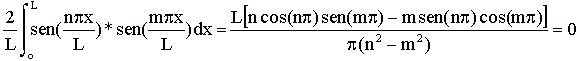 (23)
(23)
2.3 Movimento em duas Dimensões
Vamos tratar a seguir o caso do movimento de uma partícula em uma caixa de duas dimensões. Neste caso a equação de Schrödinger é igual a;
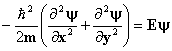 (24)
(24)
Supondo que o movimento da partícula nas duas direções são independentes, a função de onda y(x,y) pode ser decomposta em duas funções; uma em função de x e outra em função y, isto é;
![]() (25)
(25)
Substituindo esta função na equação de Schrödinger, tem-se que;
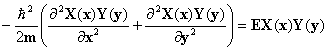 (26)
(26)
de onde se tira que;
![]() (27)
(27)
Sendo a energia total igual a soma das energia devido aos movimentos nas duas direções;
![]() (28)
(28)
As soluções das duas equações de Schrödinger, assumem a forma;
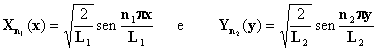 (29)
(29)
Como a função de onda total é igual ao produto das duas funções, tem-se que;
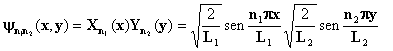 (30)
(30)
Cuja energia total é igual a;
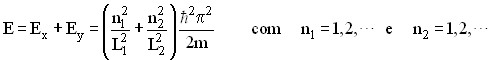 (31)
(31)
2.4 Degenerescência da Solução
No caso em que as dimensões da caixa são idênticas, isto é L1 = L2 = L, temos que;
![]() (32)
(32)
e a energia
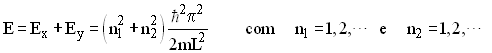 (33)
(33)
Caso n1 = 1 e n2 = 1
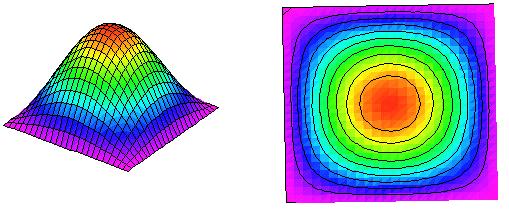
Caso n1 = 1 e n2 = 2
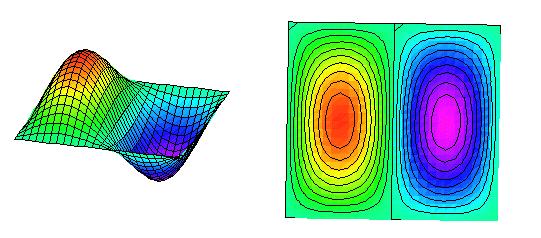
Caso n1
=
2 e n2
= 2
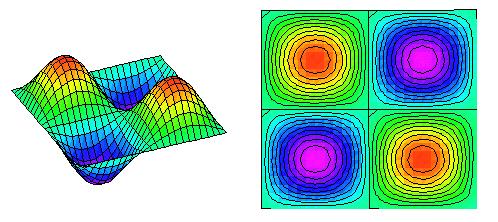
![]()
O conteúdo desta
página está em
constante atualização.
Correções no texto
e sugestões serão bem-vindas.
![]() Electronic
Address : kcmundin@unb.br
Electronic
Address : kcmundin@unb.br
Last Updated: Jul/17/2002
Copyright 1997: Kleber
C. Mundim. All rights reserved.
Register No
169.766 -
Biblioteca Nacional - Ministério da Cultura
phone: 55 61 307 2150