Capacitores com Dielérico |
Voltar à página principal |
Capacitores com Dielérico |
Voltar à página principal |
![]() Susceptibilidade e Permitividade Elétrica
Susceptibilidade e Permitividade Elétrica
Examinaremos a seguir, do ponto de vista molecular, porque a capacitância de um capacitor aumenta com a introdução de um dielétrico em seu interior. Consideremos um capacitor carregado cujas placas estão separadas pelo ar ou vácuo. Neste caso o capacitor tem carga +q em uma placa e -q na outra, como mostra a Fig.1. em seguida o capacitor é isolado da bateria. A diferença de potencial entre as placas, Vo, é dada por Vo = q/Co. Onde Co é a capacitância inicial, isto é sem a presença do dielétrico. Ao inserirmos o dielétrico no interior das placas, observamos que o dielétrico vai ficar polarizado. Este fato pode ser explicado da seguinte forma: Os átomos que não têm momento de dipolo permanente por causa de sua simetria esférica, mas, quando são colocados na presença de um campo elétrico, eles se polarizam, adquirindo um momento de dipolo induzido, na direção do campo E. Isto acontece devido à perturbação no movimento dos elétrons produzida pelo campo elétrico externo. Por outro lado, muitas moléculas têm momento de dipolo elétrico permanente e a água é um exemplo disto. Quando uma molécula polarizada é colocada na presença de um campo elétrico, ela tende a se orientar de tal forma que o seu momento de dipolo fique paralelo ao campo E. Isto é, surgirá um torque igual a;
![]() (2)
(2)
O produto entre p e E no lado direito da equação (2) é conhecido como produto vetorial. O produto vetorial entre dois vetores quaisquer produz um outro vetor que é perperndicular ao plano formado pelos dois vetores do produto. No caso da equação (2) temos então, que o torque é um vetor perpendicular simultaneamente aos dois vetores E e p.
Uma conseqüência de qualquer um desse dois efeitos é que uma porção de matéria colocada em campo elétrico torna-se eletricamente polarizada, isto é, suas moléculas (ou átomos) tornam-se dipolos elétricos orientados na direção do campo elétrico local devido à distorção do movimento eletrônico ou devido à orientação de seus dipolos permanentes. Um meio que pode ser polarizado por um campo elétrico externo é chamado dielétrico. A polarização produz uma carga resultante positiva sobre um dos lados do material e uma carga negativa resultante sobre o outro lado. Como um todo, a porção de matéria torna-se então um grande dipolo elétrico denominado de macro dipolo, o qual tende a se mover na direção em que o campo cresce.

A polarização ![]() de um material é definida como o momento de dipolo elétrico
do meio por unidade de volume. Portanto, se
de um material é definida como o momento de dipolo elétrico
do meio por unidade de volume. Portanto, se ![]() é o momento de dipolo induzido em cada átomo ou molécula
e n é o número de átomos ou moléculas por unidade
de volume, a polarização é igual a
é o momento de dipolo induzido em cada átomo ou molécula
e n é o número de átomos ou moléculas por unidade
de volume, a polarização é igual a ![]() .
.
Em geral ![]() é proporcional ao campo elétrico
é proporcional ao campo elétrico ![]() aplicado. Sendo
aplicado. Sendo ![]() medido em C/m2 ou carga por unidade de área ele é
costumeiramente escrito por;
medido em C/m2 ou carga por unidade de área ele é
costumeiramente escrito por;
![]() (3)
(3)
A quantidade ce é chamada de susceptibilidade elétrica do material. Para a maior parte das substâncias é uma quantidade positiva.

Usando a lei de Gauss podemos encontrar o campo elétrico resultante após a introdução do dielétrico no capacitor. De acordo com a Fig.9.2 temos que;
 (4)
(4)
O campo E resultante está relacionado com o campo Eo inicial por Eo = kE.
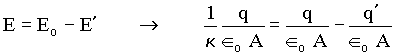 (5)
(5)
 (6)
(6)
 (7)
(7)
Onde ![]() é
o vetor deslocamento elétrico e refere-se às cargas livres,
é
o vetor deslocamento elétrico e refere-se às cargas livres, ![]() é o vetor polarização criado pelas cargas de polarização.
é o vetor polarização criado pelas cargas de polarização. ![]() é o campo elétrico resultante no interior do capacitor.
Dos resultados acima podemos derivar as seguintes equações
adicionais;
é o campo elétrico resultante no interior do capacitor.
Dos resultados acima podemos derivar as seguintes equações
adicionais;
![]() (8)
(8)
![]() (9)
(9)
onde Î/Îo = (1+c e) é a permitividade (permissividade) elétrica relativa.
- Outras relações importantes para meios isotrópicos;
 (10)
(10)![]() (11)
(11)
 (12)
(12)
![]() (13)
(13)
 (14)
(14)
 (15)
(15)
Estas equações podem ser escritas na forma matricial como a seguir;
 (16)
(16)
Portanto para meios não isotrópicos a suscetibilidade
não é um escalar, mas sim um tensor. Devemos lembrar que
no vácuo k=
1 e Î = Îo
, por esta razão a constante elétrica
Îo
é muitas vezes chamada de perssividade do
vácuo. Como a constante dielétrico k
do ar é próximo de 1, para a maioria dos propósitos,
qualquer arranjo de capacitores carregados no ar é equivalente ao
mesmo arranjo no vácuo. Lembrando que a constante dielétrica
é sempre um número puro e maior ou igual a 1. Veja a tabela
1.
|
|
Dielétrica - k |
| Vácuo |
|
| Ar | 1,00054 |
| Borracha |
|
| Papel |
|
| Porcelana |
|
| Água |
|